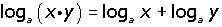Una máquina de Turing (MT) es un modelo computacional que realiza una lectura/escritura de manera automática sobre una entrada llamada cinta, generando una salida en esta misma.
Este modelo está formado por un alfabeto de entrada y uno de salida, un símbolo especial llamado blanco, un conjunto de estados finitos y un conjunto de transiciones entre dichos estados. Su funcionamiento se basa en una función de transición, que recibe un estado inicial y una cadena de caracteres (la cinta, la cual puede ser infinita) pertenecientes al alfabeto de entrada. La máquina va leyendo una celda de la cinta en cada paso, borrando el símbolo en el que se encuentra posicionado su cabezal y escribiendo un nuevo símbolo perteneciente al alfabeto de salida, para luego desplazar el cabezal a la izquierda o a la derecha (solo una celda a la vez). Esto se repite según se indique en la función de transición, para finalmente detenerse en un estado final o de aceptación, representando así la salida.
Formalmente
M = (K,Σ, δ, s)
K =Estados
Σ =Alfabeto
δ =Función de transición
s=Estado inicial
Ejemplo:
Definimos una máquina de Turing sobre el alfabeto {0,1}, donde 0 representa el símbolo blanco. La máquina comenzará su proceso situada sobre un símbolo “1″ de una serie. La máquina de Turing copiará el número de símbolos “1″ que encuentre hasta el primer blanco detrás de dicho símbolo blanco. Es decir, situada sobre el 1 situado en el extremo izquierdo, doblará el número de símbolos 1, con un 0 en medio. Así, si tenemos la entrada “111″ devolverá “1110111″, con “1111″ devolverá “111101111″, y sucesivamente. El conjunto de estados es {s1,s2,s3,s4,s5} y el estado inicial es s1. La tabla que describe la función de transición es la siguiente:
| ESTADO | S.LEIDO | S.ESCRITO | MOV. | ESTADO SIG. |
| s1 | 1 | 0 | R | s2 |
| s2 | 1 | 1 | R | s2 |
| s2 | 0 | 0 | R | s3 |
| s3 | 0 | 1 | L | s4 |
| s3 | 1 | 1 | R | s3 |
| s4 | 1 | 1 | L | s4 |
| s4 | 0 | 0 | L | s5 |
| s5 | 1 | 1 | L | s5 |
| s5 | 0 | 1 | R | s1 |
El funcionamiento de una computación de esta máquina se puede mostrar con el siguiente ejemplo (en negrita se resalta la posición de la cabeza lectora/escritora):
| PASO | ESTADO | CINTA |
| 1 | s1 | 11 |
| 2 | s2 | 01 |
| 3 | s2 | 010 |
| 4 | s3 | 0100 |
| 5 | s4 | 0101 |
| 6 | s5 | 0101 |
| 7 | s5 | 0101 |
| 8 | s1 | 1101 |
| 9 | s2 | 1001 |
| 10 | s3 | 1001 |
| 11 | s3 | 10010 |
| 12 | s4 | 10011 |
| 13 | s4 | 10011 |
| 14 | s5 | 10011 |
| 15 | s1 | 11011 |
| PARADA |
La máquina realiza su proceso por medio de un bucle, en el estado inicial s1, reemplaza el primer 1 con un 0, y pasa al estado s2, con el que avanza hasta la derecha, saltando los símbolos 1 hasta un 0 (que debe existir), cuando lo encuentra pasa a ser s3, con este estado avanza saltando los 1 hasta encontrar otro 0 (la primera vez no habría ningún 1). Una vez en el extremo derecho, añade un 1. Después comienza el proceso de retorno; con s4 vuelve a la izquierda saltando los 1, cuando encuentra un 0 (en el medio de la secuencia), pasa a s5 que continúa a la izquierda saltando los 1 hasta el 0 que se escribió al principio. Se reemplaza de nuevo este 0 por 1, y pasa al símbolo siguiente, si es un 1, se pasa a otra iteración del bucle, pasando al estado s1 de nuevo. Si es un símbolo 0, será el símbolo central, con lo que la máquina se detiene al haber finalizado su cómputo.

Un lenguaje recursivo en matemáticas, lógica e informática, es un tipo de lenguaje formal que también es llamado recursivo, decidible o Turing-decidible. Se caracterizan porque para cada uno de ellos existe una máquina de Turing que aceptará cualquier palabra del lenguaje y parará siempre.